if i prioritize to push first up, meaning always prioritize to push in the tilemap dimension first, maybe it will work? its like the "surface area" solution but with a different prioritize.
You're sort of on the right track. These steps will help, but you will still have lingering problems. For example, you can push on your prioritized axis to hopefully glide over the next tile on the other axis. However, once your player crosses a power of two boundary away from the origin the distance from one floating point value to another doubles (floating point error doubles on power of two alignment). This means as you run over tiles your prioritization will effectively make the player "float over the tiles" just fine, until randomly it doesn't work. What happens is as the player crosses a power of two boundary the next tile will have a numerically (but not visually) different position, and you will end up catching corners again.
Check this picture out from this
webpage.
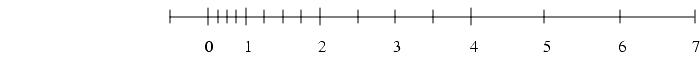
The tick marks are representing the minimum difference between two floating point numbers at different magnitudes. As you move away from the origin the floating point error doubles each time a power of two boundary is crossed.
So as you run along tiles and cross a power of two boundary, this can happen.
Even though all tiles are assigned to the same exact floating point value, due to varying magnitudes it's still going to be possible to catch edges since tiles will have slightly different x values. Not only will the tiles have slightly different x values in the example, but the behavior of the floating point x position of the player will also vary across power of two boundaries.
The implication here is that even though you might have tuned your algorithm to work well in some scenarios, it's still possible for SAT give you a MTV on the x-axis, assuming SAT finds the x-axis to be of less penetration than the y axis. Tuning will have to adjust for varying floating point errors on both the x and the y-axis as each independently varies from the origin.
One scenario may work until you walk along the x-axis far enough. Another solution might work until your player jumps to a specific tile height in the level.
It's not practical to try and hack your way around these problems. The only solution is to prevent SAT from seeing unwanted geometry at all, making it impossible to catch edges. It boils down to two options:
1. Remove internal edge geometry entirely. Something like CSG or Box2D's chain shape.
2. Use a radius of some kind. For example, rounded shapes. Somehow ensure the player is always far enough away from the internal geometry that SAT will never return internal regions as the MTV. One good way to ensure this is with swept collision detection, or careful tuning when using discrete collision detection (like low timesteps and low velocities).
The fundamental problem is that your SAT routine will still track internal edges (which means internal Voronoi regions). If you want to get rid of these without any lingering problems then you need to go back to the suggestions I made earlier, or the ones raigan (I'm assuming you're the same raigan from bullet forums?) pointed out. These solutions are eliminating internal edges and reducing the possible Voronoi regions your SAT algorithm can see.
The best solution is to not use a cube but instead use something with a curved surface. For example, a cube with a feathered radius (numerically floating), a circle, or a capsule.
Here's an example where the edge catching problem is non-existent:
https://github.com/RandyGaul/player2dAFAICT in that demo (which is really cool, thanks for sharing it!) the reason it doesn't get stuck on internal edges is because it's using swept collision -- which is another good solution to the problem of avoiding internal edges. (but which comes with its own set of tradeoffs/etc)
In my experience even if you're using circles you can get collisions with internal edges (or in that case, corners of tiles) where the order in which you collide vs the tiles matters.
You're right, the swept nature is ideal. In my experience with slower velocities, faster timesteps, and larger radii you can comfortably avoid internal edges. But, this is not an ideal solution, and does require tuning. It is an easy solution to implement though.
 Developer
Developer Technical
Technical (Moderator: ThemsAllTook)"Stuck in Corner" + Rotating Cube - Collision Problem
(Moderator: ThemsAllTook)"Stuck in Corner" + Rotating Cube - Collision Problem Developer
Developer Technical
Technical (Moderator: ThemsAllTook)"Stuck in Corner" + Rotating Cube - Collision Problem
(Moderator: ThemsAllTook)"Stuck in Corner" + Rotating Cube - Collision Problem
